Regular Expressions Based on Nondeterministic Finite Automaton

October 31, 2015 / Mad Coding, RegEx, Regular Expression, NFA

UPDATE the excellent course on Coursera by professor Robert Sedgewick also covers this with an implementation via digraph

I recently came across Russ Cox’s explanation on how many regular expression implementations behave in an exponential way in certain situations, whereas if a Nondeterministic Finite Automaton (NFA) is used then it has no such issue.

Definitely go have a read. It’s super interesting. I don’t remember if I had to convert regular expression to NFA in code when I took the compiler course. Sorry prof! But this is a nice educational exercise.

Javascript Exponential Behaviour

As explained by Russ, that the non-NFA approach is a recursive backtracking approach, which if many, many branches are encountered then it’s bad news.

What’s interesting to me is that in the data I typically come in contact with, I haven’t had this issue. I was curious if Javascript’s implementation uses backtracking. Below is a quick program I wrote to see:

'use strict';

const n = process.argv[2];

let source = '';
let regEx = '';
for (let i = 0; i < n; i++) {
    source += 'a';
    regEx += 'a?';
}
regEx += source;

const re = new RegExp(regEx);

const match = re.test(source);
if (match) {
    console.log('matches');
}
else {
    console.log("doesn't match");
}

Sure enough, just as Russ pointed out, the time it took the program to match blows up as the length of input and possible branches increase. Below is the time it took for various inputs:

command	time
./regex_builtin.js 5	0.11s
./regex_builtin.js 10	0.11s
./regex_builtin.js 15	0.12s
./regex_builtin.js 20	0.13s
./regex_builtin.js 25	0.51s
./regex_builtin.js 30	12.72s

Starting from n = 25, you already see the exponential growth. At n = 30, it took more than 12 seconds!

Convert Regular Expression to NFA

Ok, at this point I really have to see for myself the NFA approach, so I began translating his example to javascript.

1. Convert to Postfix

The first step is to convert the regular expression to postfix. So a a?a?aa regular expression becomes a?a?.a.a., where the . means concatentation in Russ’s example.

I decided to just model things as tokens since typically . in a regex already has meaning. See below:

// Character matching token
function CharacterToken(c) {
    this.c = c;
}

// Operator token for representing things like ?
function OperatorToken(op) {
    this.op = op;
}

// A special concatenation token
function ConcatenationToken() {
}

Now utilizing these classes in the convertToPostfix function, which takes a regex string and do the actual work of converting to postfix.

function convertToPostfix(re) {
    const outputQueue = [];

    // Convert a?a?aa into postfix notation
    //
    //        a
    //        a?
    //        a?a
    //        a?a?
    //        a?a?.a
    // Final: a?a?.a.a.

    let outstandingCharacterToken = 0;

    for (let i = 0; i < re.length; i++) {
        const c = re[i];
        switch (c) {
            case '?':
                // There should be an outstanding character token to apply this
                // to
                if (outstandingCharacterToken === 0) {
                    throw new Error('Invalid regular expression.');
                }
                outputQueue.push(new OperatorToken(c));
                break;

            default:
                if (outstandingCharacterToken > 1) {
                    outstandingCharacterToken--;
                    outputQueue.push(new ConcatenationToken());
                }
                outputQueue.push(new CharacterToken(c));
                outstandingCharacterToken++;
                break;
        }
    }

    while (--outstandingCharacterToken > 0) {
        outputQueue.push(new ConcatenationToken());
    }

    return outputQueue;
}

I only implemented the exact example Russ gave and skipped other possible things you can have in a regex.

2. Postfix to NFA

Once you have the regex in postfix form (e.g. a?a?.a.a., or in my case the different *Token objects), next step is to actually convert it into NFA. Below are the classes I decided to use.

MatchState

The final state indicating that the NFA matches the input data is called MatchState.

function MatchState() {
}

SplitState

SplitState is the incomplete NFA for the regex zero or one (?) operator. It has two outgoing arrows. One of which will be connected to a character token at initialization time.

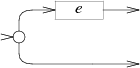
Zero or one operator graphic by Russ Cox

function SplitState(outArrow1) {
    this.outArrows = [outArrow1, null];
}

State

State is the incomplete NFA for a character token, and has only 1 outgoing arrow.

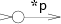
character NFA graphic by Russ Cox

function State(c) {
    this.c = c;
    this.outArrows = [null];
}

Fragment

As the regex string is converted to NFA, the Fragment class will hold the partially combined NFA produced so far. It has a start state and a list of outgoing arrows to be connected.

// Represents a combined but still incomplete NFA
function Fragment(startState, incompleteOutArrows) {
    this.startState = startState;
    this.incompleteOutArrows = incompleteOutArrows;
}

// Represent one incomplete arrow coming out from the fragment
function IncompleteArrow(state, arrowIndex) {
    this.state = state;
    this.arrowIndex = arrowIndex;
}

The Conversion

The actual process of converting from postfix to NFA is fairly simple. I think the converted javascript code is a bit easier to understand without the C pointers. The main thing to keep in mind is that Fragment is the partially combined NFA. The process mainly involves combining the incomplete NFAs and then connecting their outgoing arrows to join them. This is done via the connectArrowsToState function.

function connectArrowsToState(incompleteOutArrows, state) {
    while (incompleteOutArrows.length) {
        const incompleteArrow = incompleteOutArrows.pop();
        const arrowIndex = incompleteArrow.arrowIndex;
        incompleteArrow.state.outArrows[arrowIndex] = state;
    }
}

// Postfix tokens: a?a?.a.a.
function convertToNFA(tokens) {
    const stack = [];

    tokens.forEach(token => {

        if (token instanceof ConcatenationToken) {
            // Incomplete NFA:
            //
            // >prevFragment1--->prevFragment2--->
            //
            const prevFragment2 = stack.pop();
            const prevFragment1 = stack.pop();
            connectArrowsToState(prevFragment1.incompleteOutArrows, prevFragment2.startState);
            const newFragment = new Fragment(prevFragment1.startState, prevFragment2.incompleteOutArrows);
            stack.push(newFragment);
        }
        else if (token instanceof OperatorToken && token.op === '?') {
            // Incomplete NFA:
            //  |->prevFragment->
            // >O
            //  |--------------->
            const prevFragment = stack.pop();

            // Construct a new fragment with out arrow #1 pointing to the
            // previous fragment's state
            const state = new SplitState(prevFragment.startState);
            const incompleteArrows = prevFragment.incompleteOutArrows;
            incompleteArrows.push(new IncompleteArrow(state, 1));
            const newFragment = new Fragment(state, incompleteArrows);
            stack.push(newFragment);
        }
        else if (token instanceof CharacterToken) {
            // Incomplete NFA:
            //
            // >O---->
            //
            const state = new State(token.c);
            const incompleteArrows = [
                new IncompleteArrow(state, 0)
            ];
            const newFragment = new Fragment(state, incompleteArrows);
            stack.push(newFragment);
        }
    });

    const fragment = stack.pop();
    const matchState = new MatchState();
    connectArrowsToState(fragment.incompleteOutArrows, matchState);
    return fragment.startState;
}

3. Code to Test for Match

Now with a fully connected NFA, we can write code to pipe input through the state machine and test if things match.

As Russ explains, we’ll be simultaneously stepping through the states in multiple paths. So whether the input is a match depends on whether we’ve reached the MatchState. The function to check that is simple:

function hasMatchState(states) {
    for (let i = 0; i < states.length; i++) {
        if (states[i] instanceof MatchState) {
            return true;
        }
    }
    return false;
}

The rest is just translation from Russ’s C code, but I try to use understandable variable names. It also doesn’t have the C pointer gymnastics, which makes it easier to read the underlying algorithm.

function addState(statesList, state) {
    if (statesList.indexOf(state) >= 0) {
        return;
    }

    if (state instanceof SplitState) {
        addState(statesList, state.outArrows[0]);
        addState(statesList, state.outArrows[1]);
        return;
    }

    statesList.push(state);
}

function step(currentStates, character) {
    // Set of states the NFA will be in after processing the current character
    let nextStates = [];

    currentStates.forEach(state => {
        if (state instanceof State &&
            state.c === character) {

            addState(nextStates, state.outArrows[0]);
        }
    });

    return nextStates;
}

// Run NFA (with provided starting state) to determine whether it matches source
function nfaMatches(state, inputText) {
    // Set of states the NFA is currently in
    let currentStates = [];
    addState(currentStates, state);

    for (let i = 0; i < inputText.length; i++) {
        const c = inputText[i];
        currentStates = step(currentStates, c);
    }

    // If after processing all the input text, we arrive at the MatchState then
    // it's a match!
    return hasMatchState(currentStates);
}

function RegularExpression(regEx) {
    this.regEx = regEx;
}

RegularExpression.prototype.test = function(source) {
    const tokens = convertToPostfix(this.regEx);
    const startState = convertToNFA(tokens);
    return nfaMatches(startState, source);
};

Final Showdown

Finally putting everything together and now use RegularExpression.prototype.test function just like the built-in regex one.

'use strict';

const util = require('util');

const n = process.argv[2];

let source = '';
let regEx = '';
for (let i = 0; i < n; i++) {
    source += 'a';
    regEx += 'a?';
}
regEx += source;

const re = new RegularExpression(regEx);

const match = re.test(source);
if (match) {
    console.log('matches');
}
else {
    console.log("doesn't match");
}

The result:

command	time
./regex_nfa.js 5	0.12s
./regex_nfa.js 10	0.14s
./regex_nfa.js 15	0.13s
./regex_nfa.js 20	0.10s
./regex_nfa.js 25	0.11s
./regex_nfa.js 30	0.10s

Super fast and not exponential. Time actually decreased as n increased, but that’s just a variation in measuring based on my laptop.

This is amazing, super cool and beautiful. But it still begs the question why the default implementation doesn’t use it. Russ mentions a bunch of things to be addressed for the NFA version and perhaps that’s the hindrance. There is also the https://github.com/google/re2 library if you ever run into data that the built-in backtracking engine won’t do.

Danny Su